Properties and Applications of 2D Fourier Transform

This activity is about numerical signal filtering in Fourier space. The the goal is to work on the Fourier transform of some images, filter out the unnecessary frequency signals and then render it. Before that, we explore first two properties of 2D Fourier transform: anamorphism and rotation property.

First, I want to talk about anamorphism. The dimension of Fourier space is the inverse of the dimension of the image. This tells that what is large in image space will be small in Fourier space. This property is called anamorphism. Consider now the tall rectangle in (a) of figure 1. It has wider extent along the vertical (y) axis compared to its counterpart in horizontal (x) axis. Therefore, its Fourier transform, which is a sinc function, is wider along the x-axis compared to the y-axis as shown in figure 1b. However, when the wide rectangle is transformed, the result is a sinc function that is wider along the y-axis.

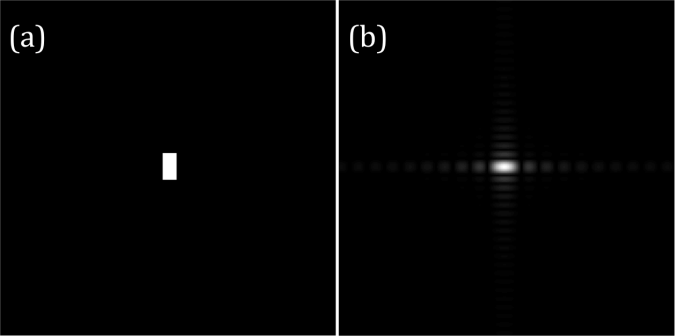
Figure 1. Tall (a) and wide (c) rectangles and their Fourier transforms (b) and (d) respectively.

To demonstrate anamorphism to other patterns, let’s have a look on the Fourier transforms of two dots with different spacing in figures 2. The Fourier transform for this case is composed of vertical bars. It is clearly seen that the as the dots become farther away from each other, the spacing of the bars in Fourier space also increases.

       Figure 2 The set of two dots in (a), (c) and (e) with different separation distances and their Fourier transforms in (b), (d), and (f) respectively.

            For the rotation property of Fourier transform, consider now a rotated sinusoid or corrugated roof about the origin. The sinusoid is z = sin(2πfy) with frequency is f = 4 Hz and its Fourier transform is composed of two Dirac deltas located on its frequency as shown in figures 3a and 3b. I also increased the frequency to 20 Hz and 30 Hz. As expected, the Dirac deltas become farther and farther apart as the frequency is increased (refer to figures 3c-e). Images has no negative values therefore to simulate a sinusoid captured by a camera, a constant bias (also known as DC signal) must be added to it. This added value has no frequency so The Fourier transform of the simulated image has a large peak on f = 0. This DC signal obscures the sinusoid signal for it has larger magnitude which is why only the central peek is visible in figure 3g. Therefore, to recover the true signal, this DC signal should be removed in Fourier space. The bias can also be a non-constant function such as another sinusoid. If this bias is added the original signal, the result is in figure 6.Its Fourier transform, However, it has 4 peaks (refer to figure 6b) pinpointing the frequencies of the original signal and the bias. To recover the original signal, the frequency of the bias must be removed in Fourier space before rendering back to the original space of the image.

Figure 3 Sinusoids with f = 4 Hz (a), 20 Hz (c) and 30 Hz (d) and their Fourier transforms (b), (d) and (e). The biased sinusoid and its Fourier transform are given , ,however, in (f) and (g).

Moving on, I rotated the sinusiod by modifying its phase term such that new function is z = sin(2πf(ysin(θ) + xcos(θ))) where θ is the rotation angle with respect to the x-axis. The sinusoid is rotated by θ = 45, 90, and 135 degrees. As a result, the Dirac deltas in Fourier space rotates as well in the same direction of θ. The rotated sinusoids and their Fourier transforms were given in figure 4.

Figure 4 Rotated sinusoids-(a), (c) and (e)- and their Fourier transforms in (b), (d) and (f).

We now investigate the transform a sinusoid multiplied with another sinusoid. Their frequencies are 4 Hz and 8 Hz respectively and the new function is u0 = sin(2π4y).*sin(2π8x). The results were presented in figure 5. The 4 off-centered peaks in Fourier space are located in points (4,8), (-4,8), (4,-8) ,and (-4,-8). Therefore, the multiplied sinusoid modulated such that their frequencies pair up forming a new set.

Figure 5 Product of two sinusoids (a) and their Fourier transform (b).

Figure 6 Sum of two sinusoids (a) and their Fourier transform (b).

Before we proceed to the image processing techniques, let’s observe first Dirac delta function and its Fourier transform. Dirac delta function is simulated by assigning one pixel to be one and the rest have 0 value. When to two Dirac deltas equidistant about the origin and placed along the x-axis are transformed in Fourier space, the result is composed of equally spaced vertical bars. When the Dirac deltas are replaced by rectangular, circular or Gaussian function, their Fourier transforms have undulations inside the envelopes which are the transforms of these objects(i.e. F{square aperture} = sinc function) as shown in figure7. However, as their dimensions become smaller, their Fourier transforms are approximately the same as the Dirac deltas’.


Figure 7 The Fourier transforms of 2 dots (a), 2 circles (b) and 2 gaussian apertures (c) are given in (d), (e) and (f) respectively.

Another exciting fact about Dirac delta is the fact that it brings the function convolved to it on its present location. I used a random 3×3 pattern to demonstrate it. It can be seen in figure 8. that the convolution of the Dirac deltas with the pattern resulted to image with miniature version of the pattern on the location of the Dirac deltas.

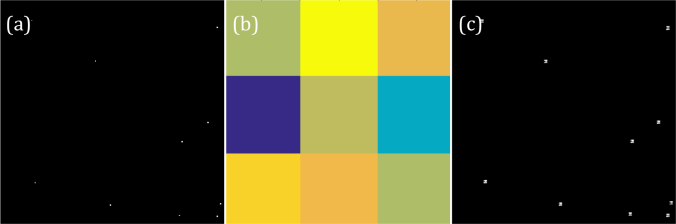
Figure 8. The convolution of Dirac deltas (a) and random pattern(b) results to (c).

Finally, the Fourier transform of an array of Dirac deltas. The contribution of the Dirac deltas along the y axis modulates the Fourier transforms of Dirac deltas lining up the x axis and forming an array of sinc functions and it is shown in figure 9. The number of bright peaks in Fourier space is equal to the number of Dirac deltas.

Figure 9. A 5×5 matrix of Dirac Deltas (a) and its Fourier transform (b)

After a long discussion about the properties of Fourier transform, we are ready to do dome image processing using this as a tool. The first image to be processed is from the Lunar Orbiter. It is a panorama with evident bright lines between each stitched frame. We want to eliminate these lines to render a smooth image. Notice that these horizontal lines occur periodically in the image. Therefore, its Fourier transform is composed of points along the y-axis. I filtered it out by blocking the signal along the y-axis of its transform and the result is a smooth picture as shown in figure 10c

Figure 10. Image from Lunar orbiter (a), its filtered Fourier transform (b) and the rendered image after filtering (c).

The next images is a picture of fingerprint. What we want is to enhance the contrast of the ridges of the patterns. The image has tightly spaced periodic patterns so the Fourier transform of this has more signal on higher frequencies. Also, the periodic lines are oblique so I expect that the frequency signals traces a round path. I filtered out the signals with lower frequencies except the DC term. The ridges become more pronounced than the previous image and it was shown in figure 11.

Figure11. Image of fingerprint (a), its filtered Fourier transform (b) and the rendered image after filtering (c).

For the last part we were tasked to obtain the canvass weave of a painting. The weave pattern is evident from the painting itself. It is a rotated periodic pattern which seems to be sinusoids that are either superimposed or multiplied to each other. Knowing this, I designed a filter that extracts the peaks corresponding to these sinusoids in Fourier space and projected it back to original plane. The result is an image of just the canvass weave. The original image of painting, its Fourier transform ,and its canvass weave are shown in figure 12

Figure 12 Image of a painting (a), its filtered Fourier transform (b) and the rendered image after filtering (c).

That was a lot of work! It was fun though knowing that how Fourier transform is so useful in image processing. My perception of as a mere long equation totally changed after this activity. I enjoyed very much and I’ve done a heck of a work. For that, I want to give myself a score of 10.

Acknowledgement:

I would like to thank Ms. Krizzia Mañago for reviewing my work.

Reference:

[1] M. Soriano, AP 186 Activity 6: Properties and Applications of 2D Fourier Transform. 2016.